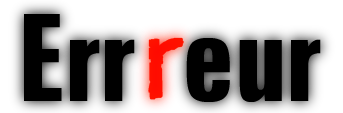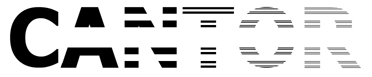Autologlyphes

Quand le sens et l'écriture renforcent ensemble l'image créée la créativité n'a plus de limite.

L'imbrication est maitrisée pour enrichir le sens.

Après avoir présenté en français les ambigrammes puis les phrases autoréférentes ou autoréférentielles, voici le travail d'un américain (Henry Segerman) sur les autologlyphes ou les mots autologiques, dont la version originale se trouve ICI . Nous qualifierons les mots autologiques ou plus "simplement" autologlyphes, des mots écrits dont le sens est contenu dans leur forme. Celle-ci pouvant être des lettres, ou plus souvent des graphies ou dessins laissant alors le champ libre à toute la créativité possible dans les domaines artistique, littéraire et scientifique.

En images ci-dessous, une succession d'exemples et leurs commentaires associés. Plusieurs graphies sont tournées autour de concepts mathématiques provenant d'esprits scientifiques parfois plus créatifs que les littéraires (cf. l'oeuvre remarquable de Douglas R. Hofstadter, et ses deux livres "GED, les brins d'une guirlande éternelle", et "Ma Thémagie").

Quelques images sont celles de ... Florian (pour Pan et Erreur), Gautier (Edison, Oeil), Louis (Peinture) et Laurine (Tony Parker, Scotch).

Sous forme de lettres, nous avons ci-dessous quelques mots autologiques voire autoréférents :

lu : effectivement, en le lisant, vous avez réalisé son sens, vous l'avez lu
mot : là aussi, ce mot n'est pas autre chose que ce qu'il dit, c'est un mot
lettres : même si c'est un mot, il ne dément pas être des lettres. Il se trouve que la succession de lettres forme le mot "lettres"
français : ce mot est effectivement un mot français
fote d'ortografe : les mots contiennent des fautes d'orthographe. Cette phrase serait donc également "réflexive"

Je vous laisse découvrir d'autres mots, en continuant avec ces exemples : écrit, polysyllabique, ..., et pourquoi pas, aller voir en librairie les deux livres de Guillaume de la Croix (dictionnaire des noms propres et dictionnaire des noms communs, où les définitions sont les dessins de chaque nom/mot).

JI LEE (http://pleaseenjoy.com) est une graphiste travaillant à NY, et ayant produit des figures dont les lettres expliquent l'image et sont imbriquées au contenu... et ce uniquement par des déformations de lettres. Voir le diaporama Ji Lee (aller aussi sur Amazon.Fr pour acheter son livre, Word as Image)

Dans la même veine, JOEL GUENOUN, graphiste français (né en 1959. Cf. www.joelguenoun.com) a fait un travail remarquable, créatif, et intelligent, régulier en fonction de l'actualité.
Voir le diaporama JOEL GUENOUN (images extraites des Mots du Mardi, Facebook).

AUTOLOGLYPHES :

Le O d'Edison est formé par le globe en verre de l'ampoule, une invention électrique de son temps, la lumière éclaire les lettres en noir.

L'entropie mesure le degré de désordre d'un système au niveau macroscopique. Plus l'entropie du système est élevée, moins ses élements sont ordonnés, liés entre eux, capables de produire des effets mécaniques, et plus grande est la part d'énergie inutilisée ou utilisée de façon incohérente. Dans cet exemple, au fur et à mesure que le mot s'écrit, il y a une dispersion des éléments microscopiques formant les lettres, et le mot devient désordonné, diffus.

Le O de Tony est un ballon de basketball, tombant dans le panier, en forme de P, commencant le nom Parker.

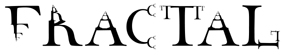L'objet fractal reprend des détails similaires à des échelles arbitrairement petites ou grandes. Il est trop irrégulier pour être décrit efficacement en termes géométriques traditionnels. Il est exactement ou statistiquement autosimilaire, c'est-à-dire que le tout est semblable à l'une de ses parties. Dans le mot "fractal" ci-dessus , en prenant par exemple la lettre C, chaque extrémité a la forme d'un C, dans laquelle chaque extrémité a elle aussi la forme d'un C, et ainsi de suite. L'ensemble des lettres répond à cette construction, typiquement fractale.

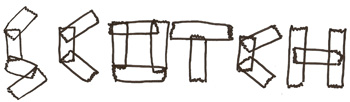
Le mot scotch est composé de segments en forme de morceaux de scotch.

Le mot et le son pan font référence à un objet qui produit ce son, ainsi qu'à la balle qui sort du révolver.

Dans le même état d'esprit, le mot tangram est formé de lettres elles-mêmes formées de sept pièces que l'on retrouve précisement dans le jeu de tangram. Il y a une parfaite unité entre la graphie et le sens du mot.

Les lettres du mot Pretzels (ou Breztels) sont formées par des biscuits salés, croquants, à base de pâte de brioche... comme la recette des bretzels.

Le mot Erreur contient en lui-même sa définition, à savoir que mettre 3 fois la lettre R est une erreur (sur le plan orthographique, pas conceptuel ou graphique).

La première lettre du mot Oeil, O, en forme ronde, est un oeil.

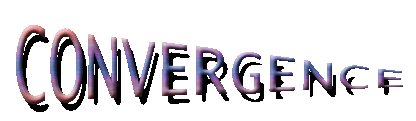Ici, le mot Convergence suit sa propre définition, de converger vers un point... celui de la fin du mot qui l'a précise ou l'a défini.

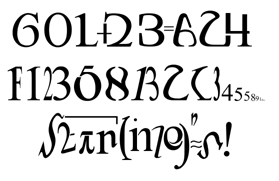Trois exemples de noms : Goldbach, Fibonacci, Stirling Goldbach : ce mathématicien allemand est plus connu pour la conjecture qui porte son nom qui affirme que "tout nombre entier pair strictement supérieur à 2 peut être écrit comme la somme de deux nombres premiers". Son nom dans l'image ci-dessus reprend ce principe : 601 + 23 = 624 (601 et 23 sont premiers). La graphie est similaire à Goldbach. Fibonacci : cette suite est construite par la somme de deux nombres formant une série commençant par un. Exemple : 1,2,3 (1+2), 5 (2+3, 8 (5+3)... Stirling : ce mathématicien anglais a publié au début du XVIIe siècle des travaux portant sur les séries infinies, l'addition, la somme, l'interpolation, et les puissances carrées ... autant de sujets représentés dans le nom dessiné ci-dessus.

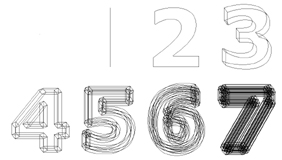Le chiffre "un" est écrit d'un bâton, tandis que 2 est composé de deux traits. etc.

Commentaires identiques à Bretzels ou Tangram, les zombies, morts-vivants dans la mythologie vaudoue, composent le mot qui les représente.

Sans jeu de mots, le noeud est imbriqué dans le mot qui lui donne sa matérialité esthétique.

Ce mathématicien d'exception a montré que l'ensemble de tous les sous-ensembles d'un ensemble A a strictement plus d'élements que A, même si A est infini, c'est-à-dire que ces deux ensembles ne peuvent être mis en bijection (il n'existe entre un ensemble A et B qu'une et une seule relation). Dans cet autologlyphe, progressivement, chaque lettre répond à ce principe, qu'il y a plus d'élements pour former une lettre. La lettre R, composée d'une multitude de fragments est néanmoins bien une lettre R.

Ici, le mot Moebius sur le ruban éponyme qui produit dans cet exemple le mot Moebius 1.5 fois la taille initiale